Forschung
Es ist nicht leicht, die Themen unserer Forschung in kurzer Form und (einigermaßen) allgemeinverständlich darzustellen. Unten folgt der Anfang eines Versuchs …
Stattdessen empfehlen wir an dieser Stelle aber auch die drei Artikel in der Zeitschrift Unikate 53 (2019), die von Mitgliedern des Essener Seminars geschrieben wurden. Die Unikate sind eine regelmäßige Publikation der Universität Duisburg-Essen. Jede Ausgabe widmet sich einem bestimmten Thema oder Themenkomplex; in Heft 53 ist das die Mathematik. Auch die Artikel aus anderen Bereichen der Fakultät sind natürlich lesenswert!
Massimo Bertolini, Kubische Kurven
Jan Kohlhaase, Kammern, Apartments, Gebäude
Das Grundthema der algebraischen Geometrie ist die Untersuchung der Lösungsmenge eines Systems von Polynomgleichungen unter geometrischen Gesichtspunkten. Zum Beispiel ist die Lösungsmenge der Gleichung $x^2+y^2=1$ in der $(x,y)$-Ebene gerade die Menge aller Punkte $(x,y)$ mit Abstand $1$ zum Ursprung – der Kreis um den Ursprung mit Radius $1$ und somit ein geometrisches Objekt.
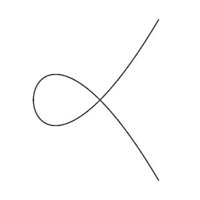 |
| Abbildung 1 |
Als zweites Beispiel betrachten wir die Gleichung $y^2 = x^2(x+1)$, deren Lösungsmenge in Abbildung 1 gezeigt wird. Eine leicht zu beschreibende geometrische Eigenschaft dieser “Kurve mit einem Knoten” ist, dass die Lösungsmenge an allen Punkten außer dem Ursprung bei starker Vergrößerung fast aussieht wie eine Gerade, sich am Ursprung jedoch zwei Zweige überkreuzen. Man nennt den Ursprung einen singulären Punkt der Kurve und die anderen Punkte glatte Punkte.
 |
 |
| Abbildung 2 | Abbildung 3 |
Gleichungen wie die der elliptischen Kurve sind auch aus zahlentheoretische Sicht interessant – in diesem Fall interessiert man sich vorrangig für Lösungen der Gleichung in der Menge der ganzen Zahlen oder der rationalen Zahlen, es zeigt sich aber, dass man auch hierfür gewinnbringende “geometrische Methoden” einsetzen kann. Die Wechselwirkung zwischen algebraische Geometrie und Zahlentheorie funktioniert sogar in beiden Richtungen. Sie dominiert einen großen Teil der modernen Zahlentheorie und hat der algebraischen Geometrie wichtige Impulse gegeben.
Themen, die speziell im Essener Seminar eine wichtige Rolle spielen, sind
Parameterräume oder Modulräume: Hier versucht man, alle Objekte einer Art (zum Beispiel alle elliptischen Kurven) durch ein anderes geometrisches Objekt zu klassifizieren, oder mit anderen Worten, die Gesamtheit dieser Objekte mit einer geometrischen Struktur zu versehen. Zum Beispiel kann man (in einem geeigneten Sinne) die Menge der elliptischen Kurven in natürlicher Weise wieder als eine Kurve (also ein eindimensionales Objekt) auffassen.
Rationale Punkte: Hier steht die Frage im Zentrum, ob eine Gleichung oder ein Gleichungssystem Lösungen in ganzen Zahlen oder in rationalen Zahlen zulässt. Wenn man andere Zahlbereiche als die reellen Zahlen zugrundelegt, lässt sich die Fragestellung weitreichend verallgemeinern. Man sucht dann Lösungen in einem kleineren Grundbereich als demjenigen, der der geometrischen Struktur zugrundeliegt.
Explizite Methoden: Einige Arbeitsgruppen, und speziell diejenigen, die am Institut für Experimentelle Mathematik angesiedelt sind, untersuchen auch, inwiefern sich theoretische Überlegungen in die Berechnung konkreter Beispiele umsetzen lassen. Einerseits kann hier die Theorie angewendet werden, um konkrete Fragen zu beantworten, andererseits liefert das gute Verständnis von Beispielen oft auch neue Anregungen für die Weiterentwicklung der Theorie.
